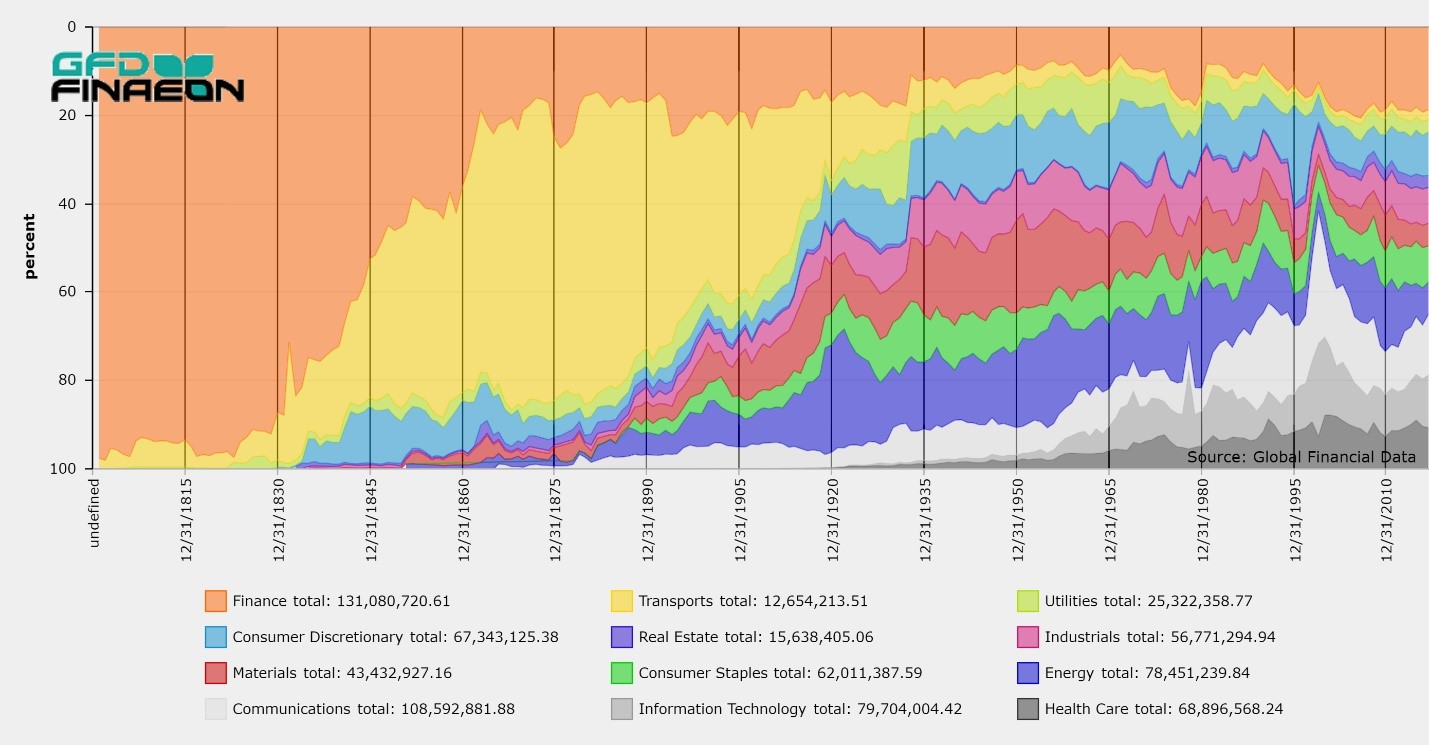
GFD is revising its stock index for Australia because it can now use data on Australian shares that were listed in London to supplement the data that already exists from Sydney and other Australian exchanges. Australia has one of the highest returns of any stock market in the world, but this is in part due to problems with the indices that were calculated in the 1950s and the biases in that data. Historical data for Australia was calculated by Lamberton in the 1950s, but the data are limited to commercial companies and ignores returns to mining and finance companies. A similar problem exists with the indices calculated by Schumann and Scheurkogel for South Africa. Once you add in the returns to finance and mining companies, Australian returns decline to a more realistic level.
The Lamberton Australian Stock Exchange Indices
When Lamberton completed his calculation of returns in 1957, he lacked the computers that were needed to create market-cap weighted indices that are now recognized as the standard for stock market index calculations. Consequently, he used short cuts that created biases in his indices. First, the price indices were unweighted giving small companies the same weight as large companies. Second, the dividend data were unweighted measures of the yield on all shares. Third, the data that were used were monthly averages rather than end-of-the-month values. Fourth, there was rapid turnover in the stocks which were few in number. In 1880, the index included just five members, and of the 40 members in 1920, just 11 remained in 1925. These four factors bias the results of the Lamberton indices. Lamberton’s biases have crept into the data in two other ways. First, most people have used the returns to commercial/industrial stocks to calculate the returns to Australian stocks and have ignored mining and finance stocks. The commercial/industrial shares had excessively high returns that exceeded the returns on finance and mining shares. Second, the calculation of dividends was equal-weighted rather than market-cap weighted. It has been estimated that Lamberton’s methodology added at least two percentage points to the actual dividend yields on Australian stocks. According to Lamberton’s calculations, the average dividend yield was 6.77% between 1882 and 1957, which is about 2 percentage points higher than the 4.45% dividend yield that was paid to British shares in London between 1882 and 1957. Lamberton also calculated three indices for stocks in Australia: mining, finance and commercial/industrial shares. The mining share index was calculated from 1875 until 1910, and during that time, mining stocks declined in price by 0.80% per annum. During the same period of time, finance stocks increased 1.57% per annum while commercial/industrial shares increased by 3.56% per annum. If you cover the full period from 1875 to 1955, annual returns on the commercial/industrial shares was 4.08% and the return on the finance shares was 1.01%. If you add the 6.77% dividend yield on commercial shares from 1882 to 1957, you get an annual return over 10% for 80 years during a period when shares in London returned 5.92% on average. Since many Australian shares traded in London, it seems hard to believe that a 4% difference in the rate of return to Australian and British shares could persist for 75 years. Why would someone invest in non-Australian shares if they knew they were going to get a 4% lower return each year? On the other hand, “real time” data exists for Australian indices between 1958 and 2018. During that period of time, share prices in Australia rose 6.23% per annum and 11.83% after dividends while inflation rose 4.67%. This gives an annual real total return of about 7% after inflation between 1958 and 2018. This is much lower than the Australian data from 1882 to 1958 and comparable to returns in the United States and other countries. By calculating indices for mining and finance shares that were listed in London, we can make direct comparisons between Lamberton’s equal-weighted results and GFD’s returns to test the validity of Lamberton’s results. To use one example, between 1887 and 1888, Lamberton’s mining index tripled in price, then lost half of its value, but GFD’s Materials index hardly budged during the same period that Lamberton’s index tripled. When we looked at the actual data, we found that over one-third of the total market cap in the GFD index came from Day Dawn Block & Wyndham Gold Mining Co. Ltd. which declined in price during that period of time, offsetting the increases in the other shares. Hence, an equal-weight index rose while the cap-weighted index remained flat. It is well known that equal-weighted indices outperform market cap-weighted indices because small companies often outperform large companies. Other examples could be provided that show how using an equal-weighted index created an upward bias in the Lamberton data. GFD has calculated return data for Australian stocks that were listed on the London Stock Exchange between 1825 and 1985. Most of the companies that were listed were finance and mining companies rather than commercial/industrial stocks. By combining the data for commercial/industrial stocks from Lamberton, the data on mining and finance stocks from GFD, and the GFD dividend data, we can obtain a data series that is more representative than the equal-weighted Lamberton data. We allocated 50% of the weight to commercial/industrial stocks and 50% to finance and mining shares. After making this change, we recalculated the Australian index and found that the price data for the GFD/Lamberton index rose by 3.19% per annum between 1882 and 1936 rather than the 4.66% increase which occurred for the Lamberton Commercial and Industrial index. Moreover, before 1875, we were able to use the returns on Australian stocks that were listed in London to extend the Australian index back another 50 years to 1825. This was when the first Australian company, the Australian Agricultural Co., listed on the London Stock Exchange. The returns to the old Australia All-Ordinaries (green) and GFD’s new All-Ordinaries (black) is illustrated in Figure 1.
The data in the file for the Australian dividend yield (SYAUSYM) reflect the dividend yields calculated by GFD from the 1830s to the 1950s while the Lamberton dividend yield data are preserved in the file SYAUSYQ. We have recalculated the Australian indices, using the combined monthly Lamberton/GFD data in the Australia ASX All-Ordinaries Price Index (_AORDD) and Return Index (_AORDAD) rather than relying purely on Lamberton as was done in the past. Because Lamberton didn’t calculate dividend yield data before 1882, the ASX All-Ordinaries Return index only goes back to 1882. With the addition of data from London, the index can begin in 1825, not 1882. Updated Stock Market Returns for Australia We divided the results into pre-Lamberton (1825-1882), Lamberton (1882-1936), and post-Lamberton eras (1936-2018). The results of the new indices are provided below.
| Nominal Price | Nominal Return | Inflation | Real Price | Real Return | Dividend Yield | ||
| Pre-Lamberton | 1825-1882 | 3.05% | 7.99% -0.17% | 3.22% | 8.18% | 4.80% | |
| Lamberton | 1882-1936 | 3.32% | 9.48% | 0.61% | 2.70% | 8.82% | 5.95% |
| Post-Lamberton | 1936-2018 | 5.53% | 12.17% | 4.93% | 0.57% | 5.99% | 5.39% |
| All Years | 1825-2018 | 4.17% | 9.77% | 2.19% | 1.94% | 7.42% | 5.37% |
The returns now seem more realistic. Using data from London between 1825 and 1882, Australian stocks returned 7.99% per annum and rose in price, on average, by 3.05% providing a dividend yield of 4.80%. The numbers are higher during the Lamberton period, though not as unrealistic as they were before. Between 1882 and 1936, the Lamberton data produced an annual nominal return of 12.09%, but with the new data, this has been reduced to 9.48%. Although the nominal return since 1936 is higher, most of this is due to inflation since the real return between 1936 and 2018 was 5.99%. Between 1958 and 2018, the real return was 6.59%. During the entire period covered, from 1825 until 2018, stocks rose in price by 4.17% before inflation and 1.94% after inflation. Including reinvested dividends, stocks returned 9.77% before inflation and 7.42% after inflation. The dividend yield was 5.37%. The real return to Australian stocks was higher before 1936 than it was after 1936, but this can be explained by the fact that Australia was an emerging market which had to compensate investors for the higher risk inestors took by investing in Australia. By comparison, between 1825 and 2018, US Stocks returned 7.10% after inflation, versus 7.42%, for Australia. Once you make these adjustments, the return on Australian stocks seems more realistic. For this reason, we will use the GFD/Lamberton data for our returns to Australia in the future. The result is illustrated in Figure 2.
Conclusion
Global Financial Data is attempting to redress some of the biases in indices that were calculated between the 1930s and 1950s before computers made it easier to calculate total returns. The only way to do this is to collect data from companies that were listed in New York and in London as well as on local exchanges and calculate the returns on those stocks. Although historical indices provided the best information that was available at the time, the indices calculated for the United States, the United Kingdom, Australia and other countries were quite limited in their methodology. They also used a small sample of shares, used monthly averages rather than monthly closes, lacked accurate dividend information, and were unable to begin their indices when shares began trading, leaving decades of stock market performance out of their calculations. Global Financial Data is attempting to correct these shortcomings and produce indices that are cap-weighted and provide both price and return indices, as well as calculation of the dividend yield, equity premium, and returns to bonds and bills. The US-100 and UK-100 indices are prime examples of what can be done with the data that GFD has collected. Australia is another example of a country whose historical indices were insufficient and for which GFD has recalculated indices to improve our estimates of past stock market behavior.